Lidar

Lidar stands for "light detection and ranging" and is a radar-related ("radiowave detection and ranging") method to remotely measure atmospheric parameters. Lidar systems send out laser pulses and detect the backscattered radiation. From the signals' time delay and the speed of light, the distance from the backscatter location can be determined. Clouds and dust particles in air (so-called aerosols) scatter laser radiation very strongly. Therefore, a simple application of lidar is the highly resolved detection and distance determination of clouds and aerosol layers. Depending on the wavelength of the laser light used, lidar systems are more or less sensible to molecular or particle backscattering. Backscattering from molecules is called Rayleigh scattering and shows a 1/λ4 proportionality. The magnitude of particle backscattering at a certain wavelength depends on particle size, refractive index and concentration of the scatterers. With lidar systems that emit multiple wavelengths, the size distribution of atmospheric particles can be determined (inversion).

A variety of atmospheric parameters can be measured with different lidar techniques: temperature, pressure, moisture (water-vapor concentration), concentration of atmospheric gases (e.g., ozone, sulfur dioxide, methane etc.). Additionally, the optical properties of cloud particles and aerosols can be determined (extinction coefficient, backscatter coefficient, depolarization) and ice and water clouds can be distinguished.

Lidar measurement principle

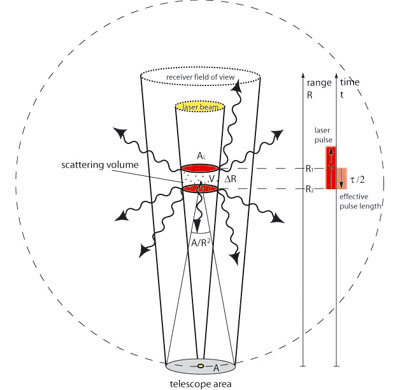
A pulsed laser beam is sent into the atmosphere, hits air molecules and other particles, and is scattered by them. The scattered light is sent into various directions and only a small part is reflected back towards its origin. The backscattered light is then collected by telescopes and conducted into a detection unit. There, after passing through filters, the signal is received by a detector (a photo multiplier tube or a photo diode), converted into electronic signals, and recorded with temporal resolution. From the time delay, the distance R of the scattering volume can be determined and is expressed as

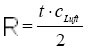
with c_Luft,the speed of light in air, and the time t between emission of the laser pulse and reception of the backscattered radiation. The maximum range resolution ΔR depends on the lenght of the laser pulse τ_L, the time constant of the detecting electronics τ_N, and the reaction time of the interaction of laser light with particles τ_W :

The time of interaction τ_W is negligible. With a typical laser pulse length of a Q-switched Nd:YAG laser τ_L = 10 ns and a time constant of the detection electronics τ_N of 50 to 200 ns, a range resolution ΔR of 7.5 to 30 m is achieved.

Lidar equation

The power P(R,λ) of the backscattered light is given by the so-called lidar equation:

The received power P(R,λ) depends on 4 terms which are listed and explained in the following table.

K - system constant:

Given that P₀ is the average power of a single laser pulse and τ the temporal pulse length, the pulse energy is derived by E₀ = P₀τ. ΔR = (cτ)/2 is the effective pulse length. A is the area of the primary reception optics and η the overall system efficiency (optical transmission from emitter to receiver and detection efficiency).

K is therefore an experimentally controlled parameter:

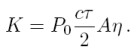
G(R) - range-dependent measurement geometry:

The geometry factor contains the overlap function of the laser beam with the receiver field of view, called O(R), and a R-2 dependence. The latter is obtained from the fact, that the area of reception is part of a sphere's surface with radius R, centered in the scattering volume.

G is also a experimentally controlled parameter:

β(R) - backscatter coefficient:

The backscatter coefficient is an atmospheric parameter which determines the strength of the lidar signal. It describes how much light is scattered in the backward direction.

Given that N_j is the concentration of scattering particles of kind j and dσ_j,sca(π,λ)/dΩ is the differential backscatter cross section of the particles, the backscatter coefficient results in the sum of all kinds of scatterers:

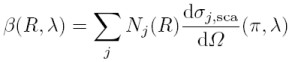
In the atmosphere, the laser light is scattered by air molecules and particles. The backscatter coefficient β(R,λ) can therefore be written as a sum:

Molecular scattering (index "mol") ist primarily dependent on air density and decreases with increasing height. The influence by particles (Index "aer") is  highly variable in space and time.

T(R) - transmission term:

That part of light which gets lost on the way from the lidar to the scattering volume is expressed by the transmission term

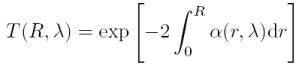
This term is derived from the specific form of the Lambert-Beer-Bouguer law for lidar. The integral describes the way from the lidar to the location of backscattering at R. The factor 2 represents the forward and backward travel of the light. The extinction coefficient α(R,λ) is computed similarly to the backscatter coefficient as a product of concentration and extinction cross section σ_{j, ext} for every type of scatterer:

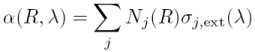
The extinction results from absorption (index "abs") and scattering (Index "sca") of light by molecules and particles:

As already mentioned, β and α depend on the wavelength of the laser light. This relation is determined by the size, refraction index, and shape of the scattering particles.

In summary, the lidar equation can be written as:

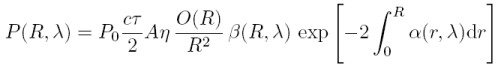
Literature

Wandinger, U. (2005), Introduction to lidar, in Lidar - Range-resolved optical remote sensing of the atmosphere, C. Weitkamp (Ed.), Springer, New York.