Lidar-Prinzip

Lidar steht für "light detection and ranging" und ist eine dem Radar ("radiowave detection and ranging") verwandte Methode zur Fernmessung atmosphärischer Parameter. Lidar-Systeme senden Laserpulse aus und detektieren das aus der Atmosphäre zurückgestreute Licht. Aus der Laufzeit der Signale und der Lichtgeschwindigkeit wird die Entfernung zum Ort der Streuung berechnet. Wolken und Staubpartikel in der Luft streuen das Laserlicht. Eine einfache Anwendung von Lidar ist daher die hochauflösende Detektion und Entfernungsmessung von Wolken und Aerosolschichten. Die Intensität der Molekül- und Partikelrückstreuung hängt von der Wellenlänge des ausgesandten Laserlichts ab. Die Rückstreuung an Molekülen, die Rayleigh-Streuung, folgt einer 1/λ⁴-Abhängigkeit. Die Stärke der Partikelrückstreuung bei einer bestimmten Wellenlänge hängt von Größe, Brechungsindex und Konzentration der Partikel ab. Mit Lidarsystemen, die mehrere Wellenlängen aussenden, kann daher die Größenverteilung der atmosphärischen Partikel bestimmt werden (Inversion).

Mit verschiedenen Lidar-Techniken lässt sich eine Vielzahl atmosphärischer Parameter messen: Temperatur, Druck, Feuchte (Wasserdampfkonzentration), die Konzentration atmosphärischer Spurengase (Ozon, Stickoxide, Schwefeldioxid, Methan usw.). Außerdem kann man die optischen Eigenschaften von Wolkenpartikeln und Aerosolen bestimmen (Extinktionskoeffizient, Rückstreukoeffizient, Depolarisation) und zwischen Wasser und Eiswolken unterscheiden.

Lidar-Messprinzip

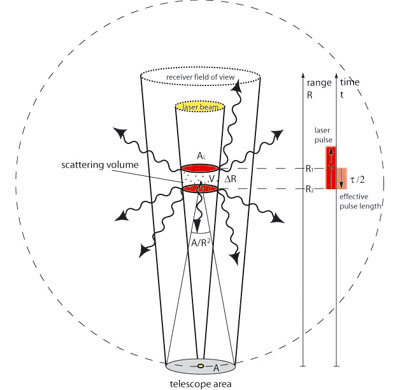
Ein gepulster Laserstrahl wird in die Atmosphäre gesandt, trifft dabei auf Luftmoleküle und Partikel (Aerosole) und wird an ihnen gestreut. Das Streulicht wird in alle Richtungen gelenkt, und ein kleiner Teil wird in Rückwärtsrichtung gestreut. Das rückgestreute Licht wird mit einem Teleskop gesammelt und in eine Detektionseinheit geleitet. Dort wird das Lichtsignal, ggf. nach Durchlaufen verschiedener Filter, mit einem Detektor (ein Photomultiplier oder eine Photodiode) erfasst, in elektrische Signale verwandelt und zeitaufgelöst aufgezeichnet.

Aus der Laufzeit des Lichts kann man die Entfernung R der Streuer ermitteln, die sich ergibt als

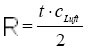
mit der Lichtgeschwindigkeit in Luft cLuft und der Zeit t zwischen Aussenden des Laserpulses und Empfangen des rückgestreuten Lichts. Die maximale Raumauflösung ΔR ist dabei abhängig von der Länge des Laserpulses τ_L, der Zeitkonstanten der Nachweiselektronik τ_N und der Reaktionszeit der Wechselwirkung des Laserlichts mit den Partikeln τ_W:

Die Reaktionszeit der Wechselwirkung τ_W ist in der Regel vernachlässigbar, so dass sich mit den etwa τ_L = 10 ns langen Laserpulsen eines gütegeschalteten Nd:YAG-Lasers und einer typischen Zeitkonstante der Nachweiselektronik τ_N von 50 bis 200 ns eine Raumauflösung ΔR von 7.5 bis 30 m erreichen lässt.

Lidargleichung

Die Leistung P(R) des rückgestreuten Lichts bei fester Wellenlänge ist gegeben durch die sogenannte Lidar-Gleichung:

Die empfangene Leistung P(R) ist abhängig von 4 Größen, die im folgenden charakterisiert sind.

K - Systemkonstante:

Unter der Annahme P₀ sei die durchschnittliche Leistung eines einzigen Laserpulses und τ die zeitliche Pulslänge, ergibt sich die Pulsenergie zu E₀ = P₀τ. ΔR = (cτ)/2 ist die effektive Pulslänge. A sei die Fläche der primären Empfangsoptik und η die gesamte Systemeffizienz (optische Transmission von Sender und Empfänger sowie Detektionseffizienz). K ist damit eine experimentell regulierbare Größe in der Form:

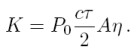
G(R) - Entfernungsabhängige Messgeometrie

Der Geometriefaktor beinhaltet die Überlappungsfunktion von Laserstrahl und Empfänger-Gesichtsfeld, die Funktion O(R), und den Term R-2. Letzterer leitet sich daraus ab, dass die Empfangsfläche den Teil einer Kugelfläche mit dem Radius R in dieser Entfernung vom Streuort ausmacht.

G ist damit eine experimentell regulierbare Größe der Form:

β(R) - Rückstreukoeffizient:

Der Rückstreukoeffizient ist ein atmosphärischer Parameter, der die Stärke des Lidarsignals bestimmt. Er beschreibt, wie viel Licht in die Rückwärtsrichtung gestreut wird.

Ist N_j die Konzentration der streuenden Partikel der Sorte j und dσ_j,sca(π,λ)/dΩ der differentielle Rückstreuquerschnitt der Partikel, ergibt sich der Rückstreukoeffizient als Summe über alle Streuer j:

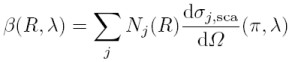
In der Atmosphäre wird das Laserlicht von Luftmolekülen sowie von Partikeln gestreut. Der Rückstreukoeffizient β(R,λ) kann deshalb auch als Summe

geschrieben werden. Molekulare Streuung (Index "mol") ist hauptsächlich von der Luftdichte abhängig und sinkt damit mit steigender Höhe. Der Beitrag durch Partikel (Index "aer") ist sowohl räumlich als auch zeitlich hochgradig variabel.

T(R) - Transmissionsterm:

Der Teil des Lichts, der auf dem Weg vom Lidar zum Streuvolumen und zurück verloren geht, wird durch den Transmissionsterm

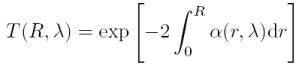
beschrieben. Dieser Ausdruck folgt aus der speziellen Form des Lambert-Beer-Bouguer-Gesetzes für Lidar. Das Integral beschreibt dabei den Weg vom Lidar zum Ort der Rückstreuung R. Der Faktor 2 steht für den Hin- und Rückweg. Der Extinktionskoeffizient α(R,λ) wird ähnlich dem Rückstreukoeffizienten als ein Produkt aus Konzentration und Extinktionsquerschnitt σ_j, ext für jeden Typ von Streuer in dieser Form gebildet:

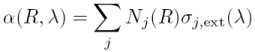
Die Extinktion ergibt sich durch Absorption (Index "abs") und Streuung (Index "sca") von Licht durch Moleküle und Partikel:

Wie bereits angedeutet, hängen β und α von der Wellenlänge des Laserlichts ab. Diese Abhängigkeit wird bestimmt durch die Größe, den Brechungsindex und die Form der streuenden Partikel.

Somit ergibt sich die Lidargleichung über das Einsetzen der einzelnen Parameter zu:

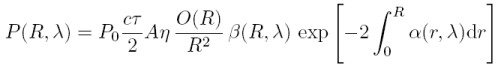
Weiterführende Literatur

Wandinger, U. (2005), Introduction to lidar, in Lidar - Range-resolved optical remote sensing of the atmosphere, C. Weitkamp (Ed.), Springer, New York.