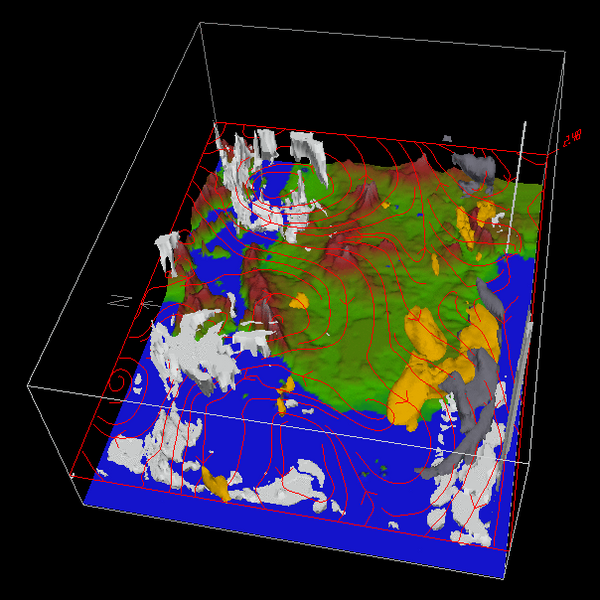
Modellsimulation von Wolken (weiß), Windfeldern (rote Linien), Brandaerosol (grau) und Mineralstaub (gelb) über Westaftrika und dem Atlantik. Quelle: Bernd Heinold/TROPOS

Das Chemie-Transport Model COSMO-MUSCAT

Modellsimulation von Wolken (weiß), Windfeldern (rote Linien), Brandaerosol (grau) und Mineralstaub (gelb) über Westaftrika und dem Atlantik. Quelle: Bernd Heinold/TROPOS
Überblick
COSMO-MUSCAT ist ein modernes mesoskaliges Chemie-Transport-Modell für Prozessstudien und Luftqualitätsanwendungen (Wolke et al., 2012). Das online-gekoppelte System besteht aus dem regionalen Wettermodell COSMO (COnsortium for Small scale MOdelling) und dem Chemie-Transportmodell MUSCAT (MUltiScale Chemistry Aerosol Transport). COSMO, das bis 2020 das operationelle Vorhersagemodell des Deutschen Wetterdienstes (DWD) war, löst die Atmosphärengleichungen auf der Basis eines geländefolgenden Gitters (Schättler et al., 2018; Baldauf et al., 2011). Angetrieben durch das meteorologische Modell, behandelt MUSCAT den atmosphärischen Transport und die chemischen Umwandlungen für verschiedene Gasphasenspezies und Aerosolpartikelpopulationen. Sein Kern basiert auf Massenbilanzen, die durch ein System von zeitabhängigen, dreidimensionalen Advektions-Diffusions-Reaktionsgleichungen beschrieben werden.
MUSCAT enthält aktuelle Emissionssparametrisierungen für natürliches Aerosol, wie Wüstenstaub (Heinold et al., 2011; Schepanski et al., 2017) und Aerosol aus Meeresgischt (Barthel et al., 2019), sowie ein hochentwickeltes Schema für biogene Emissionen (Luttkus et al., 2021). Die Bildung von sekundärem organischem Aerosol (SOA) und komplexe mehrphasige chemische Prozesse werden sehr detailliert berücksichtigt (Schrödner et al., 2014; Luttkus et al., 2021). Aerosolpartikel können im meteorologischen Modell mit Wolken und Strahlung interagieren und auf die atmosphärische Dynamik einwirken. Die anthropogenen Emissionen von Primärpartikeln und Vorläufern von Sekundäraerosolen werden aus aktuellen Katastern vorgegeben. Die Transportprozesse umfassen Advektion, turbulente Diffusion, Sedimentation, trockene und nasse Deposition. Die antreibenden Windfelder sowie die vertikalen Diffusionskoeffizienten und Grenzschichtwiderstände werden online vom COSMO bereitgestellt (Raschendorfer, 2001). Darüber hinaus ist das Modell mit der Double Canyon Effect Parametrization (DCEP; Schubert et al., 2012) ausgestattet, um in urbanen Simulationen die Auswirkungen der Stadtmorphologie auf die Luftströmung und Strahlung zu berücksichtigen.
COSMO-MUSCAT wird regelmäßig für Luftqualitätsanwendungen eingesetzt (z.B. Stern et al., 2007; Hinneburg et al., 2009; Renner und Wolke, 2010; Wolke et al., 2012; Luttkus et al., 2021). Darüber hinaus wird das Modell in verschiedenen wissenschaftlichen Studien eingesetzt, in denen zum Beipiel die direkten und halbdirekten Strahlungseffekte absorbierenden Aerosols untersucht werden (z.B. Heinold et al., 2011; Meier et al., 2012; Banks et al., 2018) oder der Einfluss von Aerosolpartikeln auf das Budget von Wolkenkondensations- (Dipu et al., 2017) und Eiskeimen (Weger et al., 2019). 2019 wurde COSMO-MUSCAT erstmals für eine operationelle Luftqualitätsvorhersage für die Stadt Leipzig und das östliche Mitteldeutschland eingesetzt, um eine Feldkampagnen mit Bürgerwissenschaftlern zu begleiten (Tõnisson et al., 2021).
Mehrere Modellvergleichsstudien bestätigen die gute Performance des Modellsystems, z.B. die internationalen Modellevaluierungsinitiative AQMEII (Solazzo et al., 2012 a,b; Im et al. 2014 a,b).
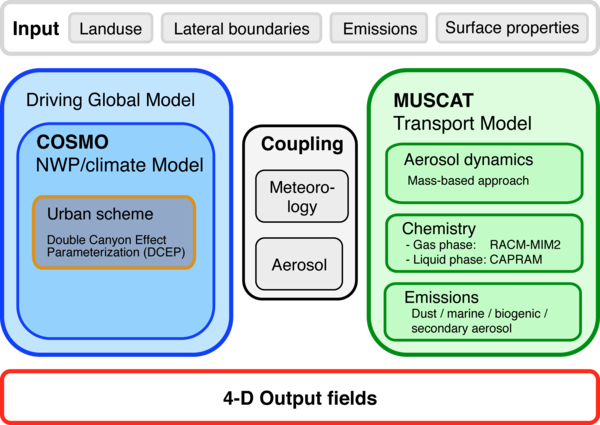
Auf einen Blick. Schema des multiskaligen Chemie-Transport-Modells COSMO-MUSCAT.
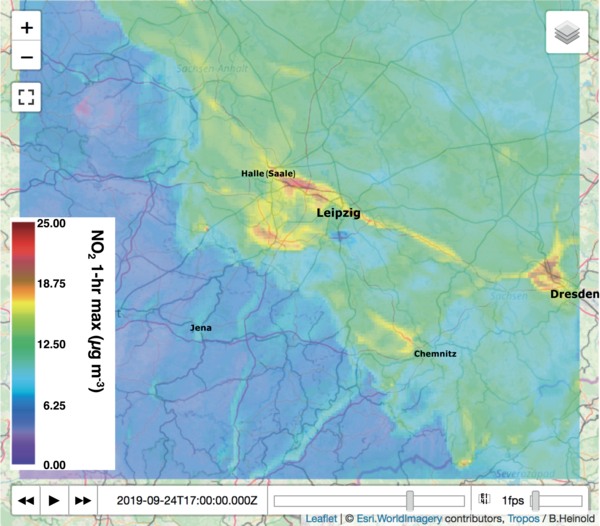
Maximale stündliche NO2-Belastung über Mitteldeutschland aus der quasioperationellen Vorhersage mit COSMO-MUSCAT für den 24.09.2019. Screenshot der interaktiven Webkarte, die im Rahmen des Bürgerwissenschaftsprojekts WTimpact bereitgestellt wurde.
Atmosphärische Aerosole und Spurengase
Mulitphasenchemie. Gasphasenprozesse, einschließlich der Bildung von Photooxidantien sowie des Transports und der Umwandlung von Partikeln, werden berücksichtigt. Chemische Reaktionsmechanismen werden aus ASCII-Dateien importiert. Alle Informationen, die für die Berechnung der chemischen Terme und der zugehörigen Jacobi-Matrix benötigt werden, werden aus einer solchen Mechanismusdatei generiert. Änderungen im chemischen Mechanismus sind daher einfach und umfassend möglich. Mehrere Gasphasenmechanismen, z.B. RACM-MIM2-ext (Stockwell et al., 1997; Karl et al., 2006; Luttkus et al., 2021) mit mehr als 90 Spezies und über 200 Reaktionen, wurden erfolgreich in 3D-Fallstudien eingesetzt. Seit kurzem kann auch die Gasphasenchemie durch den aktuellen MOZART4/JAM-002-Mechanismus mit über 200 Spezies und über 500 Reaktionen beschrieben werden (Schultz et al., 2018). Alle Gasphasenmechanismen behandeln den Abbau von biogenen und anthropogenen flüchtigen Verbindungen (VOCs) mit unterschiedlicher Komplexität. Ein wichtiges Thema bei der chemischen Umwandlung von VOCs ist ihre Auswirkung auf die Ozonkonzentration (O3), die in MUSCAT berücksichtigt werden soll.
Die Bildung von sekundärem organischen Aerosol (SOA) wird durch das Aerosolmodul SORGAM (Schell, et al., 2001) beschrieben, das um zusätzliche Produktionswege erweitert wurde, darunter die Reaktionen von Monoterpenen mit NO3 (Griffin et al., 1999), Isopren (Kroll et al., 2006; Ng et al., 2008), Ses-Quiterpen (Hoffmann et al., 1997; Karl et al., 2009b) sowie die Bildung von hoch oxygenierten organischen Molekülen (HOMs) aus allen betrachteten BVOCs (Monoterpen: Berndt et al., 2016a; Jokinen et al., 2015; Sesquiterpene: Richters et al., 2016; Isopren: Berndt et al., 2016b). Tests zeigten, dass diese Modellerweiterungen die Übereinstimmung von simulierten und gemessenen Konzentrationen organischer Stoffe deutlich verbessern (Luttkus et al., 2021).
Die sekundäre anorganische Aerosolbildung wird aus Reaktionen zwischen Ammoniak und Schwefel- oder Salpetersäure berechnet, die aus den Gasphasenvorläufern SO2 und NOX gebildet werden (Hinneburg et al., 2009). Die angewandte Partikel/Gas-Partitionierung hängt von der Temperatur und der Luftfeuchtigkeit ab. Wie in ISORROPIA (Nenes et al., 1998) wird das Gleichgewicht bei trockenen und warmen Bedingungen in Richtung Gasphase verschoben. Die Realisierung ist vergleichbar mit Galperin und Sofiev (1998) und nutzt den Gleichgewichtsansatzes von Mozurkewich (1993). Die N2O5-Hydrolyse, die eine wichtige Quelle für Aerosolnitrat in der Troposphäre ist, wird nach Chen et al. (2018) parametrisiert.
Die in der MUSCAT-Chemie verwendeten Photolyseraten werden in der Mechanismusdatei als Raten für unbewölkten Himmel im reaktionsspezifischen Wellenlängenbereich gemäß den MCM-Vorschriften angegeben und sind vom solaren Zenitwinkel abhängig (Saunders et al. 2003). Abschattungsfaktoren für die Reduktion der Photolyseraten aufgrund von Wolken werden aus COSMO-Diagnostiken der vertikal aufgelösten Wolkenbedeckung und der hohen Wolkenbedeckung für Schichten oberhalb der MUSCAT-Domain berechnet (Eppel et al., 1995). Die modellierte Aerosol- und Ozonkonzentration wird derzeit nicht berücksichtigt.
Für eine detaillierte Beschreibung der Chemie der wässrigen Phase wurde ein reduziertes CAPRAM-Schema in das Modellsystem integriert (Schrödner et al., 2014; 2018).
Aerosoldynamik. Es gibt zwei Ansätze zur Beschreibung der verschiedenen Aerosolpopulationen in MUSCAT. Zum einen gibt es ein hybrides Bulk-Bin-Schema, das als Standardkonfiguration für Luftqualitätssimulationen eingesetzt wird. Es umfasst 25 prognostische Partikel-Tracer, darunter primäres PM2,5 und PM10, primärer organischer Kohlenstoff (POC), schwarzer Kohlenstoff (BC), Sulfataerosol, Nitrat und Ammonium, sekundäres organisches Aerosol (SOA) sowie sechs Bins für Meersalz und primäre marine organische Partikel (Durchmesserbereich: 0,01-10 µm) und fünf Wüstenstaub-Bins (0,2-48 µm). Die verschiedenen Aerosolarten werden als extern gemischt betrachtet. Außerdem kann das modale Aerosolschema M7 (Vignati et al., 2004), erweitert um die Behandlung von Nitrat und Ammonium, zur Beschreibung der Partikelgrößenverteilung und der dynamischen Aerosolprozesse eingesetzt werden. Bei diesem Ansatz wird die gesamte Partikelpopulation aus sieben lognormalen Modi mit unterschiedlichen Zusammensetzungen aggregiert, die von der Größe und Löslichkeit der Aerosolpartikel abhängen. Die Größenverteilung entwickelt sich aufgrund externer dynamischer Aerosolprozesse wie Partikeltransport durch Konvektion und Diffusion, Ablagerung und Sedimentation sowie aufgrund interner Prozesse wie Kondensation und Koagulation.
Anthropogene Emissionen. Die zeitlich aufgelösten anthropogenen Emissionen werden als Punkt-, Flächen- und Linienquellen behandelt. Die zeitliche Entwicklung der anthropogenen Emissionen wird im Hinblick auf die Intensität anhand von Zeitprofilen betrachtet, wobei zwischen den verschiedenen Emissionssektoren unterschieden wird. Die verschiedenen Quellenarten (z.B. Energieumwandlung, industrielle Verbrennung, Straßenverkehr, Landwirtschaft) können entweder in Form von SNAP-Codes (Selected Nomenclature of Air Pollution) oder unter Verwendung der GNFR-Klassifizierung (Gridded Nomenclature For Reporting) für die Quellensektoren angegeben werden. Die Emissionsdateien von Gasen und Aerosolen innerhalb von MUSCAT werden von Präprozessoren erzeugt. Innerhalb Europas wird das regionale Kataster anthropogenenr Aerosol- und Spurengasemissionen CAMS-REG (Kuenen et al., 2014; Granier et al., 2019; eccad3.sedoo.fr) des Copernicus Atmosphere Monitoring Service (CAMS) verwendet, während außerhalb Europas die Luftschadstoffemissionen auf dem EDGARv5-Datensatz (Crippa et al., 2018) basieren. Zusätzlich werden die Emissionen aus der Biomasseverbrennung mit täglichen Daten aus dem Global Fire Assimilation System (GFAS; Kaiser et al., 2012) vorgegeben. Für Anwendungen in Deutschland werden Punkt- sowie detaillierte Flächen- (550 m native Auflösung) und Straßenemissionen aus der GRETA-Datenbank des Umweltbundesamtes (UBA; Scheider et al., 2016) verwendet. Die zeitlichen Emissionsprofile für die wichtigsten Luftschadstoffe und die Treibhausgase basieren durchgängig auf dem CAMS-REG-TEMPO-Datensatz für Europa und Deutschland.
Biogene Emissionen. Landwirtschaftliche Flächen können eine wichtige Quelle für Stickoxide sein, die durch mikrobiologische Prozesse verursacht werden. Die NO-Emissionen des Bodens werden anhand empirischer Beziehungen parametrisiert, die von der Art der Landnutzung, der jahreszeitlichen Phänologie und der Bodentemperatur abhängen. Die funktionale Abhängigkeit folgt Williams et al. (1992) und Stohl et al. (1996).
Für die BVOC-Emissionen wird das Modell von Steinbrecher et al. (2009) verwendet, das die Abhängigkeit von meteorologischen Parametern (photosyntheseaktive Strahlung, Temperatur) und der Landnutzung berücksichtigt: (1) Fläche einer bestimmten Landnutzungskategorie, (2) zugehörige Biomassedichte (BD) und (3) Standardemissionspotenzial (SEP bei 30°C und photosyntheseaktiver Strahlung von 1000 mol m 2 s 1) für verschiedene BVOC sowie die Saisonalität. Die Werte für das landwirtschaftliche BD wurden anhand von Oderbolz et al. (2013) aktualisiert. Die betrachteten BVOC-Emissionen umfassen Isopren, 17 Monoterpene (z.B. alpha- und beta-Pinen, Limonen), Sesquit-Erepene und sauerstoffhaltige BVOCs (z.B. Alkohole, Aldehyde). Jede BVOC-Spezies hat einen spezifischen Reaktionsgeschwindigkeitskoeffizienten für die Reaktion mit Ozon, OH- und NO3-Radikalen und kann somit das atmosphärische Oxidationspotenzial beeinflussen. Die Stärke und Zusammensetzung der BVOC-Emissionen variiert erheblich zwischen den Landnutzungsarten/Baumarten aufgrund des damit verbundenen BD und ihres BVOC-spezifischen SEP. Das Standard-Setup verwendet einen Datensatz mit 10 Landnutzungsklassen: Wasser, Watt, Sand, gemischte Landnutzung (hauptsächlich Landwirtschaft), Wiesen, Heide, Gebüsch, Mischwald, Nadelwald und Stadtgebiet. Zusätzlich wurde ein neuer, detaillierterer Landnutzungsdatensatz eingeführt, der 138 Landnutzungsklassen mit 116 Baumarten und 11 landwirtschaftlichen Landnutzungstypen umfasst (Köble und Seufert, 2001). Eine Sensitivitätsstudie unter Verwendung der beiden Setups zeigte, dass eine zu allgemeine Modelldarstellung der Landnutzung mit nur einer einfachen Kat-egorisierung in gemischte Landnutzung, Nadel- und Mischwälder regional zu 50% überschätzten BVOC-Emissionen (Isopren, Mono- und Sesquiterpene) führt, was zu veränderten Oxidationsmittelkonzentrationen (NOx 2,5%, Ozon +2,5%, OH 50%, NO3-Radikal -70%) und einer Überschätzung von SOA um bis zu 60% führt (Luttkus et al., 2021). Für OzonEval werden die CORINE-Landbedeckungsdaten verwendet, die ähnliche landwirtschaftliche Landnutzungsklassen wie der Datensatz von Köble und Seufert et al. (2001), jedoch verallgemeinerte Waldkategorien enthalten.
Windbedingte Aerosolemissionen. Als die beiden Hauptkomponenten des natürlichen Aerosols werden in MUSCAT Wüstenstaub und Meeresgischtaerosol online berechnet. Die Berechnung der Mobilisierung von Wüstenstaub verwendet die aktuellen Windfelder und hydrologischen Bedingungen aus dem COSMO-Modell und berücksichtigt die Bodentextur und die Bodengrößenverteilung nach Tegen et al. (2002) sowie präferenzielle Quellregionen (Heinold et al., 2011; Schepanski et al., 2017). Die Meersalzemissionen werden mit einer Parametrisierung nach Long et al. (2011) unter Berücksichtigung der Abhängigkeit von der Meeresoberflächentemperatur nach Sofiev et al. (2011) berechnet. In Verbindung mit dem Meersalz basiert die Emission von primärem marinen Aerosol auf der Verteilung von marinem Chlorophyll-a (Barthel et al., 2019).
Trocken- und Nassdeposition. Die trockene Deposition wird mit Hilfe des von Seinfeld und Pandis (2006) beschriebenen Widerstandsansatzes modelliert, der die atmosphärische Turbulenz, die kinetische Viskosität und die Ablagerung von Partikeln durch die Schwerkraft berücksichtigt. Die Berechnung beinhaltet den quasi-laminaren, den turbulenten Rauhigkeits- und den turbulenten Prandtl-Schicht-(aerodynamischen)Widerstand, die jeweils online aus COSMO (Raschedorfer, 2001; Baldauf et al., 2011) übernommen werden und somit direkt von der Grenzschichtentwicklung und den Landoberflächeneigenschaften des meteorologischen Antriebsmodells abhängen. Darüber hinaus wird der Oberflächenwiderstand in Abhängigkeit von der Landnutzung parametrisiert (Schlünzen & Pahl 1991; Schlünzen et al. 2012). Aerosolpartikel und Spurengase werden zudem durch Nassdeposition aus der Atmosphäre entfernt, wobei zwischen In-Cloud und Below-Cloud Scavenging unterschieden wird. Beide Prozesse werden in Form von größenabhängigen Sammeleffizienzen für Partikel und entsprechenden Aufnahmekoeffizienten für Gase parametrisiert (Simpson et al., 2012).
Numerik
Multiblock-Gitterstruktur. In MUSCAT ist eine statische horizontale Gitterstaffelung (Wolke und Knoth, 2000; Knoth und Wolke, 1998b) implementiert. Das meteorologische Modell COSMO verwendet ein gedrehtes sphärisches Gitter mit einer hybriden vertikalen Koordinate. Um das horizontale Gitter über alle Prozessoren zu verteilen, wird es in rechteckige Partitionen mit einer möglichst gleichen Anzahl von Gitterzellen zerlegt. Das MUSCAT-Gitter basiert auf dem des COSMO, ist aber in sogenannte Blöcke unterteilt, die unterschiedliche horizontale Auflösungen haben können. Diese Multiblocktechnik wird eingesetzt, um die Rechenkosten in weniger interessanten Grenzregionen zu reduzieren und sich auf bestimmte Regionen von Interesse, wie Kraftwerke und städtische Gebiete, mit einer feineren Auflösung zu konzentrieren. Die räumliche Diskretisierung erfolgt durch ein Finite-Volumen-Schema auf einem gestaffelten Gitter. Solche Schemata sind dafür bekannt, dass sie aufgrund der direkten Diskretisierung der Integralform der Erhaltungssätze massenkonservativ sind. Für die Approximation der Oberflächenintegrale werden Punktwerte der Durchmischung und ihrer ersten Ableitung auf den Zellflächen benötigt. Zur Approximation des Mischungsverhältnisses an der Oberfläche wird sowohl ein Upwind Verfahren erster Ordnung als auch ein Upwind-biased Verfahren dritter Ordnung mit zusätzlicher Begrenzung eingesetzt (Hundsdorfer et al., 1995). Dieses Verfahren muss auf nicht-äquidistante Stencil angewendet werden, die an der Schnittstelle von Blöcken mit unterschiedlichen Auflösungen auftreten (Knoth und Wolke, 1998b). Die Partitionen in MUSCAT werden durch die Zuordnung von Blöcken zu Prozessoren gebildet. Diese Zuordnung wird mit Hilfe der Gitterpartitionierungsbibliothek ParMETIS (Karypis et al., 2003) bestimmt. Sie minimiert die Länge der Partitionsgrenzlinien ("edge cut"), während die Anzahl der Gitterzellen jedes Prozessors ausgeglichen wird. Je mehr Blöcke für die Dekomposition verwendet werden, desto feiner kann die Anzahl der Gitterzellen ausbalanciert werden.
Zeitintegrationsschema. MUSCAT verwendet ein implizit-explizites (IMEX) Zeitintegrationsschema (Knoth und Wolke, 1998b; Wolke und Knoth, 2000), um den langsamen Prozess der horizontalen Advektion und die schnellen Prozesse des vertikalen Austauschs und der Gasphasenchemie auf effiziente Weise zu kombinieren. Während die langsamen Prozesse durch explizite Runge-Kutta-Methoden integriert werden, kann für die schnellen Prozesse jeder geeignete Solver verwendet werden. Diskontinuitäten im Lösungsprozess wie beim konventionellen Operator-Splitting werden bei diesem Ansatz vermieden. Im Rahmen der impliziten Integration im Chemie-Transport-Code MUSCAT werden die starre Chemie und alle vertikalen Transportprozesse (turbulente Diffusion, Advektion, Deposition) gekoppelt mit der BDF-Methode zweiter Ordnung integriert. Wir verwenden eine Modifikation des Codes LSODE (Hindmarsh, 1983) mit einem speziellen linearen Systemlöser und einem angepassten Restart-Verfahren (Knoth und Wolke, 1998a). Die Fehlerkontrolle kann zu mehreren impliziten Zeitschritten pro explizitem Schritt führen. Außerdem können in verschiedenen Blöcken unterschiedliche implizite Schrittgrößen erzeugt werden. Die Größe des "großen" expliziten Zeitschritts hängt von der CFL-Zahl ab. Durch die Wahl unterschiedlicher Advektionsschritte in verschiedenen Modellregionen kann insbesondere in Fällen mit wenigen großen Punktquellen eine signifikante Reduktion der Rechenkosten erreicht werden (Schlegel et al., 2012a, b).
Online Kopplung Meteorologie-Chemie. Im Modellsystem COSMO-MUSCAT können alternativ zwei unterschiedliche Kopplungsstrategien verwendet werden (Lieber und Wolke, 2008). Beim parallelen Ansatz laufen beide Modellcodes weitgehend unabhängig voneinander auf jeweils einer eigenen disjunkten Menge von Prozessoren. Die Anzahl der Prozessoren für Meteorologie und Chemie-Transport muss bei der Modellinitialisierung festgelegt werden. Da in MUSCAT eine adaptive Zeitschrittsteuerung eingesetzt wird, schwankt die Gesamtauslastung während der Laufzeit, insbesondere bei Szenarien mit hochdynamischem Verhalten der simulierten chemischen Prozesse. Diese Schwankungen führten zu Leerlaufzeiten des Prozessors an den Synchronisationspunkten der beiden Modelle. Schwankungen der gesamten MUSCAT-Arbeitslast führten zu Leerlaufzeiten der Prozessoren an den Synchronisationspunkten der beiden Modelle. Um eine höhere Effizienz zu erreichen, wurde ein alternatives Kopplungsschema implementiert, das auf dem "sequentiellen" Ansatz basiert (Lieber und Wolke, 2008). Die Vorteile sind eine erhöhte Leistung und ein vereinfachter Modellaufbau, da keine Prozessorpartitionierung (Bestimmung der Prozessoren für COSMO und MUSCAT) a priori festgelegt werden muss. Dadurch, dass diese entscheidende Entscheidung nicht getroffen werden muss, wird eine potenzielle Quelle der Ineffizienz beseitigt. Die Codes werden nur für den Datenaustausch zwischen COSMO und MUSCAT synchronisiert. Dies geschieht nur in jedem expliziten Zeitschritt (Paarzeitschritt). Da dieser Zeitschritt als ein Bruchteil der CFL-Zahl gewählt wird, variiert seine Länge über die Vorhersagezeit. Abb. 4 zeigt das Kopplungsschema.
Parallelisierung und dynamisches Load-Balancing. Der Code wird parallelisiert, indem die Blöcke (rechteckige Teilmengen des Gitters) mit MPI auf die verfügbaren Prozessoren verteilt werden. Eine statische Aufteilung kann zu Lastungleichgewichten führen, da jeder Block seine eigene Zeitschrittgröße hat, die durch den impliziten Zeitintegrator definiert ist. Daher wurde ein dynamischer Lastausgleich entwickelt, der die Blöcke periodisch umverteilt. Die Graphpartitionierungsbibliothek ParMETIS (Karypis et al., 2003) wird verwendet, um eine verbesserte Partitionierung aus der Arbeitslast der Blöcke und ihrer Nachbarschaft zu berechnen.
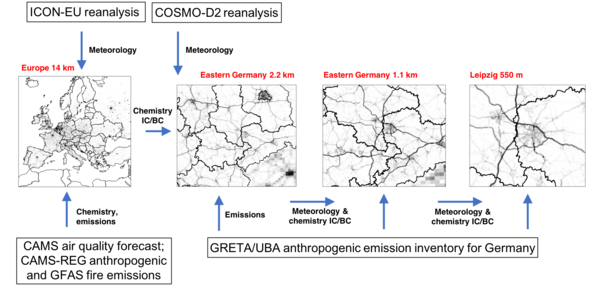
Nestungskette für die Luftqualitätsmodellierung mit COSMO-MUSCAT für die Stadt Leipzig.
Standard-Konfiguration
Luftqualitätssimulationen mit COSMO-MUSCAT werden typischerweise in einem genesteten Ansatz durchgeführt. Ausgehend von einer äußeren Domain wird die horizontale Auflösung schrittweise von 14 km über Europa auf 2 - 4 km über Deutschland sowie auf etwa 500 m für die innersten Domain erhöht, die das Stadtgebiet und die Umgebung einer Stadt von Interesse abdeckt. In der Vertikalen wird das Modell mit einer höhenbasierten, geländefolgenden Koordinate mit mit der Höhe zunehmender Schichtdicke genutzt. Für die Rechengebiete mit einem Gitterabstand von 14 km, 2 - 4 km bzw. 500 m wird ein Setup mit 40, 65 und 60 Schichten verwendet, mit 11, 20 und 23 vertikalen Schichten innerhalb der untersten 1000 m. Die unterste Schicht reicht bis 20 m über den Boden und 7 m für das 500-m-Gebiet. Die Modelloberkante in COSMO befindet sich in etwa 22 km über Grund und 15 km für das 500-m-Gebiet, während die vertikale Koordinate von MUSCAT auf 8 km Höhe begrenzt ist. Die äußerste Domäne, die die Hintergrundkonzentrationen von Aerosolen und chemischen Stoffen über Deutschland liefert, wird von der ICON-EU-Reanalyse des Deutschen Wetterdienstes (DWD) angetrieben. Die CAMS-Modellvorhersage liefert den Input für die Aerosol- und Gas-Randbedingungen der groben Domäne. Die meteorologischen Ausgangs- und Randdaten für das Gebiet über Deutschland mit 2,2 km Gitterabstand stammen aus der DWD-Reanalyse COSMO-D2 oder ICON-D2. Für die beiden folgenden Domänen mit einer Gitterweite von 1,1 km bzw. 550 m werden die Randbedingungen des jeweils gröberen Modelllaufs verwendet. Für die europäische Domäne werden die anthropogenen Luftschadstoffemissionen auf der Grundlage des CAMS-REG-Katasters und die Landnutzung durch die auf CORINE 2000 basierenden EU-JRC-Daten mit detaillierten Baumarteninformationen von Köble und Seufert (2001) vorgegeben, während für Deutschland die GRETA-Emissionen bzw. die ESA GlobCover 2009-Datenbank verwendet werden. Die Modellläufe werden alle 48 bis 72 Stunden reinitialisiert, um die Meteorologie nahe an den realen Wetterbedingungen zu halten. Nach 24 Stunden Anlaufzeit (Spin up) für COSMO wird MUSCAT gekoppelt, um die Chemie- und Transportprozesse zu berechnen. Der erste Zyklus einer Simulationsperiode beginnt mit festen Anfangskonzentrationen oder CAMS-Luftverschmutzungsfeldern; die folgenden Zyklen werden mit den Spurengas- und Aerosolfeldern des vorherigen Laufs initialisiert, um eine kontinuierliche Simulation zu gewährleisten.
Referenzen
Baldauf, M., Seifert, A., Förstner, J., Majewski, D., Raschendorfer, M. & Reinhardt, T. (2011). Operational convective-scale numerical weather prediction with the COSMO model: description and sensitivities. Mon. Weather Rev. doi:10.1175/MWR-D-10-05013.1.
Banks, J. R., Schepanski, K., Heinold, B., Hünerbein, A., and Brindley, H. E.: The influence of dust optical properties on the colour of simulated MSG-SEVIRI Desert Dust infrared imagery, Atmos. Chem. Phys., 18, 9681–9703, doi.org/10.5194/acp-18-9681-2018, 2018.
Barthel, S., Tegen, I. & Wolke, R. (2019). Do new sea spray aerosol source functions improve the results of a regional aerosol model? Atmos. Environ., 198, 265-278. doi.org/10.1016/j.atmosenv.2018.10.016.
Berndt, T., Herrmann, H., Sipilä, M., & Kulmala, M. (2016). Highly Oxidized Second-Generation Products from the Gas-Phase Reaction of OH Radicals with Isoprene. J. Phys. Chem. A, 120, 10150–10159. doi.org/10.1021/acs.jpca.6b10987.
Berndt, T., Richters, S., Jokinen, T., Hyttinen, N., Kurtén, T., Otkjær, R. V., et al. (2016). Hydroxyl radical-induced formation of highly oxidized organic compounds. Nat. Comm., 7(13677), 1–8. doi.org/10.1038/ncomms13677.
Chen, Y., Wolke, R., Ran, L., Birmili, W., Spindler, G., Schröder, W., Su, H., Cheng, Y., Tegen, I., & Wiedensohler, A. (2018). A parameterization of the heterogeneous hydrolysis of N2O5for mass-based aerosol models: improvement of particulate nitrate prediction. Atmos. Chem. Phys., 18, 673–689. doi.org/10.5194/acp-18-673-2018, 2018.
Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener, F., van Aardenne, J. A., Monni, S., Doering, U., Olivier, J. G. J., Pagliari, V., & Janssens-Maenhout, G. (2018). Gridded emissions of air pollutants for the period 1970–2012 within EDGAR v4.3.2. Earth Syst. Sci. Data, 10, 1987–2013. doi.org/10.5194/essd-10-1987-2018.
Dipu, S., Quaas, J., Wolke, R., Stoll, J., Mühlbauer, A., Sourdeval, O., Salzmann, M., Heinold, B. & Tegen, I. (2017). Implementation of aerosol–cloud interactions in the regional atmosphere–aerosol model COSMO-MUSCAT(5.0) and evaluation using satellite data.Geosci. Model Dev., 10, 2231-2246. doi.org/10.5194/gmd-10-2231-2017.
Eppel, D. P., Kapitza, H., Claussen, M., Jacob, D., Koch, W., Levkov, L., Mengelkamp, H.-T. & Werrmann, N. (1995). The Non-Hydrostatic Mesoscale Model GESIMA. Part II: Parameterizations and Applications, Beitr. Phys. Atmosph., 68, 15-41.
Galperin, M. V. & Sofiev, M. A. (1998). The long-range transport of ammonia and ammonium in the northern hemisphere. Atmos. Environ. 32, 373-380.
Gatzsche, K., Iinuma, Y., Tilgner, A., Mutzel, A., Berndt, T. & Wolke, R. (2017). Kinetic modeling studies of SOA formation from α-pinene ozonolysis. Atmos. Chem. Phys., 17, 13187–13211. doi.org/10.5194/acp-17-13187-2017.
Granier, C., S. Darras, H. Denier van der Gon, J. Doubalova, N. Elguindi, B. Galle, M. Gauss, M. Guevara, J.-P. Jalkanen, J. Kuenen, C. Liousse, B. Quack, D. Simpson & K. Sindelarova (2019). The Copernicus Atmosphere Monitoring Service global and regional emissions (April 2019 version). Report April 2019 version. doi:10.24380/d0bn-kx16.
Griffin, R. J., Cocker III, D. R., Flagan, R. C., & Seinfeld, J. H. (1999). Organic aerosol formation from the oxidation of biogenic hydrocarbons. J. Geophys. Res.: Atmos., 104(D3), 3555–3567. doi.org/10.1029/1998JD100049.
Heinold, B., Tegen, I., Schepanski, K., Tesche, M., Esselborn, M., Freudenthaler, V., Gross S., Kandler K., Knippertz, P., Müller, D., Schladitz, A., Toledano, C., Weinzierl, B., Ansmann, A., Althausen, D., Müller, T., Petzold, A. & Wiedensohler, A. (2011). Regional modelling of Saharan dust and biomass-burning smoke Part 1: Model description and evaluation. Tellus B, 63(4), 781-799. doi:10.1111/j.1600-0889.2011.00570.x.
Hindmarsh, A. C. (1983). ODEPACK: A systematized collection of ODE solvers. In: R. S. Stepleman, Ed., Scientific Computing, pages 55–74.
Hinneburg, D., Renner, E. & Wolke, R. (2009). Formation of secondary inorganic aerosols by power plant emissions exhausted through cooling towers in Saxony. Environ. Sci. Pollut. Res., 16, 25-35.
Hoffmann, T., Odum, J. R., Bowman, F., Collins, D., Klockow, D., Flagan, R. C., & Seinfeld, J. H. (1997). Formation of Organic Aerosols from the Oxidation of Biogenic Hydrocarbons. J. Atmos. Chem., 26(2), 189–222. doi.org/10.1023/A:1005734301837.
Hundsdorfer, W., Koren, B., van Loon, M. & Verwer, J. G. (1995). A positive finite-difference advection scheme. J. Comput. Phys. 117, 35–46.
Im, U., Bianconi, R., Solazzo, E., Kioutsioukis, I., Badia, A. et al. (2014a). Evaluation of operational online-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2. Part I: Ozone. Atmos. Environ., 115, 404-420. doi.org/10.1016/j.atmosenv.2014.09.042.
Im, U., Bianconi, R., Solazzo, E., Kioutsioukis, I., Badia, A., et al. (2014b). Evaluation of operational online-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2. Part II: Particulate matter. Atmos. Environ., 115, 420-441, doi:10.1016/j.atmosenv.2014.08.072.
Jokinen, T., Berndt, T., Makkonen, R., Kerminen, V.-M., Junninen, H., Paasonen, P., et al. (2015). Production of extremely low volatile organic compounds from biogenic emissions: Measured yields and atmospheric implications. PNAS, 112(23), 7123–7128. doi.org/10.1073/pnas.1423977112.
Kaiser, J. W., Heil, A., Andreae, M. O., Benedetti, A., Chubarova, N., Jones, L., Morcrette, J.-J., Razinger, M., Schultz, M. G., Suttie, M. & van der Werf, G. R. (2012). Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power, Biogeosciences, 9, 527–554. doi.org/10.5194/bg-9-527-2012.
Karl, M., Dorn, H.-P., Holland, F., Koppmann, R., Poppe, D., Rupp, L., Schaub, A., Wahner, A. (2006). Product study of the reaction of OH radicals with isoprene in the atmosphere simulation chamber, SAPHIR. J. Atmos. Chem., 55, 167-187.
Karl, M., Guenther, A., Koble, R., Leip, A., & Seufert, G. (2009a). A new European plant-specific emission inventory of biogenic volatile organic compounds for use in atmospheric transport models. Biogeoscience, 6, 1059–1087. doi.org/10.5194/bg-6-1059-2009.
Karl, M., Tsigaridis, K., Vignati, E., & Dentener, F. (2009b). Formation of secondary organic aerosol from isoprene oxidation over Europe. Atmos. Chem. Phys., 9(18), 7003–7030. doi.org/10.5194/acp-9-7003-2009.
Karypis, G., Schloegel, K. & Kumar, V. (2003). ParMETIS: Parallel graph partitioning and sparse matrix ordering library (Version 3.1). University of Minnesota.
Kioutsioukis, I., Im, U., Solazzo, E., Bianconi, R., Badia, A., et al. (2016). Insights into the deterministic skill of air quality ensembles from the analysis of AQMEII data, Atmos. Chem. Phys., 16, 15629–15652. doi.org/10.5194/acp-16-15629-2016.
Knoth, O. & R. Wolke (1998a). An explicit-implicit numerical approach for atmospheric chemistry-transport modelling. Atmos. Environ. 32, 1785-1797.
Knoth, O. & R. Wolke (1998b). Implicit-explicit Runge-Kutta methods for computing atmospheric reactive flows, Appl. Numer. Math. 28, 327–341.
Köble, R., & Seufert, G. (2001). Novel Maps for Forest Tree Species in Europe. Paper presented at Proceedings of the 8th European Symposium on the Physico-Chemical Behaviour of Air Pollutants: "A Changing Atmosphere!", Torino, Italy.
Kroll, J. H., Ng, N. L., Murphy, S. M., Flagan, R. C., & Seinfeld, J. H. (2006). Secondary Organic Aerosol Formation from Isoprene Photooxidation. Environ. Sci. Technol., 40(6), 1869–1877. doi.org/10.1021/es0524301.
Kuenen, J. J. P., Visschedijk, A. J. H., Jozwicka, M. & Denier van der Gon, H. A. C. (2014). TNO-MACC_II emission inventory; a multi-year (2003–2009) consistent high-resolution European emission inventory for air quality modelling. Atmos. Chem. Phys., 14, 10963–10976. doi.org/10.5194/acp-14-10963-2014.
Lieber, M. & Wolke, R. (2008). Optimizing the coupling in parallel air quality model systems. Environ. Model. Softw., 23, 235-243.
Long, M. S., Keene, W. C., Kieber, D. J., Erickson, D. J. & Maring, H. (2011). A sea-state based source function for size- and composition-resolved marine aerosol production. Atmos. Chem. Phys., 11, 1203–1216. doi:10.5194/acp-11-1203-2011.
Luttkus, M. L., Hoffmann, E. H., Poulain, L., Tilgner, A. & Wolke, R. (2021). The effect of land use classification on the gas-phase and particle composition of the troposphere: tree species vs. forest information. J. Geophys. Res.: Atmos., submitted.
Meier, J., Tegen, I., Heinold, B. & Wolke, R. (2012). Direct and semi-direct radiative effects of absorbing aerosols in Europe: Results from a regional model. Geophys. Res. Lett., 39, L09802. doi:10.1029/2012GL050994.
Mozurkewich, M. (1993). The dissociation constant of ammonium nitrate and its dependence on temperature, relative humidity and particle size. Atmos. Environ., 27 A, 261-270.
Ng, N. L., Kwan, A. J., Surratt, J. D., Chan, A. W. H., Chhabra, P. S., Sorooshian, A., et al. (2008). Secondary organic aerosol (SOA) formation from reaction of isoprene with nitrate radicals (NO3). Atmos. Chem. Phys., 8(14), 4117–4149. https://doi.org/10.5194/acp-8-4117-2008.
Oderbolz, D. C., Aksoyoglu, S., Keller, J., Barmpadimos, I., Steinbrecher, R., Skjøth, C. A., et al. (2013). A comprehensive emission inventory of biogenic volatile organic compounds in Europe: improved seasonality and land-cover. Atmospheric Chemistry and Physics, 13(4), 1689–1712. doi.org/10.5194/acp-13-1689-2013.
Raschendorfer, M. (2001). The new turbulence parameterization of LM. COSMO Newsletter, 1, 89–97.
Renner, E. & Wolke, R., (2010). Modelling the formation and atmospheric transport of secondary inorganic aerosols with special attention to regions with high ammonia emissions. Atmo. Environ., 44, 1904-1912.
Richters, S., Herrmann, H., & Berndt, T. (2016). Highly Oxidized RO2Radicals and Consecutive Products from the Ozonolysis of Three Sesquiterpenes. Environ. Sci. Technol., 50(5), 2354–2362. doi.org/10.1021/acs.est.5b05321.
Saunders, S. M., Jenkin, M. E., Derwent, R. G. & Pilling, M. J. (2003). Protocol fort he development oft he Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds. Atmos. Chem. Phys., 3, 161-180. doi.org/10.5194/acp-3-161-2003.
Schättler, U., Doms, G. &Schraff, C. (2018). A Description of the Nonhydrostatic Regional COSMO-Model. Deutscher Wetterdienst, Offenbach. www.cosmo-model.org.
Schell, B., Ackermann, I. J., Hass, H., Binkowski, F. S., & Ebel, A. (2001). Modeling the formation of secondary organic aerosol within a comprehensive air quality model system. J. Geophys. Res.: Atmos.,106(D22), 28275–28293. doi.org/10.1029/2001JD000384.
Schepanski, K., Heinold, B. & Tegen, I. (2017). Harmattan, Saharan heat low, and West African monsoon circulation: modulations on the Saharan dust outflow towards the North Atlantic. Atmos. Chem. Phys., 17, 10223-10243. doi.org/10.5194/acp-17-10223-2017.
Schlegel, M., Knoth, O., Arnold, M. & Wolke, R. (2012a). Implementation of multirate time integration methods for air pollution modelling. Geosci. Model Dev., 5, 1395–1405. doi.org/10.5194/gmd-5-1395-2012.
Schlegel, M., O. Knoth, M. Arnold, & R. Wolke (2012b). Numerical solution of multiscale problems in atmospheric modeling. Appl. Numer. Math., 62(10), 1531-1543. doi:10.1016/j.apnum.2012.06.023.
Schlünzen, K. H. & Pahl, S. (1991). MODIFICATION OF DRY DEPOSITION IN A DEVELOPING SEA-BREEZE CIRCUATION-A NUMERICAL CASE STUDY. Atmospheric Environment., 26A(1), 51-61. https://doi.org/10.1016/0960-1686(92)90260-R.
Schlünzen, K. H., Bungert, U., Flagg, D. D., Fock, B. H., Gierisch, A. et al. (2012). Technical Documentation oft he Multiscale Model System M-SYS (METRAS, MITRAS, MECTM, MICTM, MESIM). MEMI Technical Report 3, Meteorologisches Institut, KlimaCampus, Universität Hamburg.
Schneider C., Pelzer, M., Tönges-Schuller, N., Nacken, M. & Niederau, A. (2016). ArcGIS basierte Lösung zur detaillierten, deutschlandweiten Verteilung (Gridding) nationaler Emissionsjahreswerte auf Basis des Inventars zur Emissionsberichterstattung, Umweltbundesamt UBA-FB-002360, Texte 71/2016, ISSN 1862-4804.
Schrödner, R., Tilgner, A., Wolke, R. & Herrmann, H. (2014). Modeling the multiphase processing of an urban and a rural air mass with COSMO–MUSCAT. Urban Clim., 10(4), 720-731. doi.org/10.1016/j.uclim.2014.02.001.
Schrödner, R., Wolke, R., Tilgner, A., van Pinxteren, D. & Herrmann, H. (2018). Modelling multiphase aerosol-cloud processing with the 3-D CTM COSMO-MUSCAT: Application for cloud events during HCCT-2010. Mensink, C., Kallos, G. (Ed.), In: Air pollution modeling and its application XXV: Proceedings of the 35th International Technical Meeting on Air Pollution Modelling and Its Application (Chania, Crete, Greece, 3-7 October 2016), Springer International Publishing, Cham, Switzerland, p. 587-592. doi:10.1007/978-3-319-57645-9.
Schubert, S., Grossman-Clarke, S. & Martilli, A. (2012). A Double-Canyon Radiation Scheme for Multi-Layer Urban Canopy Models. Bound.-Lay. Meteorol., 145, 439–468. doi:10.1007/s10546-012-9728-3.
Schultz, M. G., Stadtler, S., Schröder, S., Taraborrelli, D., Franco, B., et al. (2018). The chemistry–climate model ECHAM6.3-HAM2.3-MOZ1.0. Geosci. Model Dev., 11, 1695–1723. doi:10.5194/gmd-11-1695-2018, 2018.
Seinfeld, J. H. & Pandis, S. N. (2006). Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. 2nd ed., John Wiley & Sons, New York.
Simpson, D., Benedictow, A., Berge, H., Bergström, R., Emberson, L. D., et al. (2012). The EMEP MSC-W chemical transport model – technical description. Atmos. Chem. Phys., 12, 7825–7865. doi.org/10.5194/acp-12-7825-2012.
Sofiev, M., Soares, J., Prank, M., deLeeuw, G., & Kukkonen, J. (2011). A regional to global model of emission and transport of sea salt particles in the atmosphere. J. Geophys. Res.: Atmos., 116. doi.org/10.1029/2010JD014713.
Solazzo, E., Bianconi, R., Vautard, R., Appel, K. W., Moran, M. D., et al. (2012a). Ensemble modelling of surface level ozone in Europe and North America in the context of AQMEI. Atmos. Environ., 53, pp. 60-74.
Solazzo, E., Bianconi, R., Pirovano, G., Matthias, V., Vautard, R., et al. (2012b). Operational model evaluation for particulate matter in Europe and North America in the context of AQMEII. Atmos. Environ., 53 (2012), pp. 75-92.
Steinbrecher, R., Smiatek, G., Köble, R., Seufert, G., Theloke, J., Hauff, K., et al. (2009). Intra- and inter-annual variability of VOC emissions from natural and semi-natural vegetation in Europe and neighbouring countries. Atmos. Environ.,43(7), 1380–1391. doi.org/10.1016/j.atmosenv.2008.09.072.
Stern, R., Builtjes, P., Schaap, M., Timmermans, R., Vautard, R., Hodzic, A., Memmesheimer, M., Feldmann, H., Renner, E., Wolke, R. & Kerschbaumer, A. (2008). A model intercomparison study focussing on episodes with elevated PM10 concentrations. Atmos. Environ., 42, 4567-4588.
Stockwell, W. R., Kirchner, F., Kuhn, M., & Seefeld, S. (1997). A new mechanism for regional atmospheric chemistry modeling. J. Geophys. Res.: Atmos., 102(D22), 25847–25879. doi.org/10.1029/97JD00849.
Stohl, A., Williams, E., Wotawa, G., & Kromp-Kolb, H. (1996). A European inventory of soil nitric oxide emissions and the effect of these emissions on the photochemical formation of ozone. Atmos. Environ., 30(22), 3741–3755. doi.org/10.1016/1352-2310(96)00104-5.
Tegen, I., Harrison, S. P., Kohfeld, K. E., Prentice, I. C., Coe, M. C. & Heimann, M. (2002). The impact of vegetation and preferential source areas on global dust aerosol: results from a model study. J. Geophys. Res., 107. doi:10.1029/2001JD000963.
Tõnisson, L., Voigtländer, J., Weger, M., Assmann, D., Käthner, R., Heinold, B. & Macke, A. (2021). Knowledge Transfer with Citizen Science: Luft-Leipzig Case Study. Sustainability, 13, 7855. doi.org/10.3390/su13147855.
Vignati, E., Wilson, J. & Stier, P. (2004). M7: An efficient size resolved aerosol microphysics module for large scale aerosol transport, J. Geophys. Res.: Atmos., 109. doi.org/10.1029/2003JD004485.
Weger, M., Heinold, B., Engler, C., Schumann, U., Seifert, A., Fößig, R., Voigt, C., Baars, H., Blahak, U., Borrmann, S., Hoose, C., Kaufmann, S., Krämer, M., Seifert, P., Senf, F., Schneider, J. &Tegen, I. (2018). The impact of mineral dust on cloud formation during the Saharan dust event in April 2014 over Europe. Atmos. Chem. Phys., 18, 17545–17572. doi.org/10.5194/acp-18-17545-2018.
Williams, E. J., Guenther, A., & Fehsenfeldi, F. C. (1992). An inventory of nitric oxide emissions from soils in the United States. J. Geophys. Res.: Atmos., 97(D7), 7511–7519. doi.org/10.1029/92JD00412.
Wolke, R., and Knoth, O., Implicit-explicit Runge-Kutta methods applied to atmospheric chemistry-transport modelling, Environ. Model. Softw., 15, 711–719, 2000.
Wolke, R., and Knoth, O., Time-integration of multiphase chemistry in size-resolved cloud models, Appl. Numer. Math., 42(1-3), 473–487, doi:10.1016/S0168-9274(01)00169-6, 2002.
Wolke, R., Schröder, W., Schrödner, R. and Renner, E. (2012). Influence of grid resolution and meteorological forcing on simulated European air quality: a sensitivity study with the modeling system COSMO–MUSCAT. Atmos. Environ., 53, 110–130. doi.org/10.1016/j.atmosenv.2012.02.085.